| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Adapter 패턴
- 안드로이드 웹뷰
- CORDA
- Hyperledger fabric gossip protocol
- play 강좌
- 파이썬 강좌
- 스칼라
- 파이썬 데이터분석
- akka 강좌
- 스칼라 동시성
- 하이브리드앱
- Play2
- 파이썬 머신러닝
- Actor
- 파이썬 동시성
- 파이썬
- Play2 로 웹 개발
- 엔터프라이즈 블록체인
- Golang
- 스칼라 강좌
- 블록체인
- hyperledger fabric
- 그라파나
- 이더리움
- Akka
- 스위프트
- 하이퍼레저 패브릭
- play2 강좌
- 플레이프레임워크
- 주키퍼
- Today
- Total
목록파이썬 (8)
HAMA 블로그
Python 과 Mixin 파이썬은 다중 상속을 지원하며 그것에 의해 Mixins 를 만들 수 있다. Mixin 은 클래스에 추가적인 속성이나 메소드를 제공하는 것을 말하는데, 스칼라는 traits 를 통해서 제공하며, 루비등도 제공한다. 파이썬은 Mixin 을 위한 특별한 키워드는 없으며, 단지 다중상속을 통해서 만들기 때문에 이 과정에서 문제가 생길 소지가 생긴다. 스칼라의 경우 stackable traits pattern이라고 동일한 메소드가 있을 경우 순서대로 하나씩 실행되지만 파이썬의 경우 덮어 써 버린다. 다음 예를 살펴보자 class Mixin1(object): def test(self): print "Mixin1" class Mixin2(object): def test(self): prin..
 파이썬 코딩으로 말하는 데이터 분석 - 7. 회귀분석 (최소제곱법,경사하강법)
파이썬 코딩으로 말하는 데이터 분석 - 7. 회귀분석 (최소제곱법,경사하강법)
순서 1. 통계 - 카운팅,min,max,평균,중앙값,산포도,분산,편차,공분산,상관관계 2. 가설과 추론 (베이지언 - 사후확률,우도) 3. 군집화 (K-Means)4. 연관 (Apriori)5. 함수형으로 데이터 다루기 6.경사하강법7. 회귀분석8. 은닉 마코프법 (HMM) 9. k-NN10. DTW * 참고로 "밑바닥부터 배우는 데이터과학" 서적은 numpy,scikit-learn 등의 외부라이브러리를 활용은 배제되었습니다. 회귀분석 Okky 싸이트에 들어오는 사람들이 Okky 싸이트에 머무는 시간과 그들의 경력에 대해서 생각해보자.머무는 시간이 1시간이면 , 경력은 5년 머무는 시간이 2시간이면, 경력은 7년 ..이렇게 데이터가 누적되었을때, 그 둘 간의 어떠한 상관관계가 있는지 살펴봐서 , 머무는..
 파이썬 코딩으로 말하는 데이터 분석 - 6. 경사하강법
파이썬 코딩으로 말하는 데이터 분석 - 6. 경사하강법
요즘 데이터분석과 관련하여 텐서플로우와 스파크(ML)등의 머신러닝 솔루션들이 굉장히 유행하고 있습니다. 물론 저것들이 삶을 편안하게 만들어주기도 하지만 대부분의 데이터 분석은 저런 거창한 것 말고 평균,편차 같은 기본적인 개념으로 부터 시작되고 있으며 이러한 개념을 조금씩 변경해가며 더 의미있는 가치를 찾기 위해 빠르게 적용해보는 과정을 거쳐야하는데 그러기 위해서는 1. 직접 코딩해서 기본적인 데이터분석 유틸리티 함수들을 만들어봐야한다. 2. SQL문을 잘 다루어야한다. 3. 엑셀을 잘 다루어야 한다. 이 3가지는 기본이라고 저는 생각합니다. 소규모 데이터를 가지고 이리저리 반복해서 돌려보는 과정은 매우 중요하며 이런 기본적인 것들도 못하면서 하둡,텐서플로우나 깔짝대고, 데이터 분석 한다 라고 칭할 수는..
순서 1. 통계 - 카운팅,min,max,평균,중앙값,산포도,분산,편차,공분산,상관관계 2. 가설과 추론 (베이지언 - 사후확률,우도) 3. 군집화 (K-Means)4. 연관 (Apriori)5. 함수형으로 데이터 다루기 6. 경사하강법7. 회귀분석8. 은닉 마코프법 (HMM) 9. k-NN10. DTW * 참고로 "밑바닥부터 배우는 데이터과학" 서적은 numpy,scikit-learn 등의 외부라이브러리를 활용은 배제되었습니다. 데이터 다루기 대부분의 언어들이 함수형을 차용하고 있으며 , 파이썬도 빠질리는 없다. 파이썬의 함수형 도구들을 사용하여 데이 터 분석을 해보자.참고: 파이썬, C++ ,Java 8은 모두 기본적으로는 객체지향언어에 가깝지만 모두 함수형 파라다임을 차용하고 있다. 스칼라 같은 언..
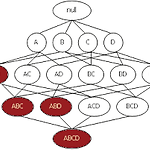 파이썬 코딩으로 말하는 데이터 분석 - 4. 연관 (Apriori 알고리즘)
파이썬 코딩으로 말하는 데이터 분석 - 4. 연관 (Apriori 알고리즘)
요즘 데이터분석과 관련하여 텐서플로우와 스파크(ML)등의 머신러닝 솔루션들이 굉장히 유행하고 있습니다. 물론 저것들이 삶을 편안하게 만들어주기도 하지만 대부분의 데이터 분석은 저런 거창한 것 말고 평균,편차 같은 기본적인 개념으로 부터 시작되고 있으며 이러한 개념을 조금씩 변경해가며 더 의미있는 가치를 찾기 위해 빠르게 적용해보는 과정을 거쳐야하는데 그러기 위해서는 1. 직접 코딩해서 기본적인 데이터분석 유틸리티 함수들을 만들어봐야한다. 2. SQL문을 잘 다루어야한다. 3. 엑셀을 잘 다루어야 한다. 이 3가지는 기본이라고 저는 생각합니다. 소규모 데이터를 가지고 이리저리 반복해서 돌려보는 과정은 매우 중요하며 이런 기본적인 것들도 못하면서 하둡,텐서플로우나 깔짝대고, 데이터 분석 한다 라고 칭할 수는..
순서 1. 통계 - 카운팅,min,max,평균,중앙값,산포도,분산,편차,공분산,상관관계 2. 가설과 추론 (베이지언 - 사후확률,우도) 3. 군집화 (K-Means)4. 연관 (Apriori)5. 함수형으로 데이터 다루기 6. 경사하강법7. 회귀분석8. 은닉 마코프법 (HMM) 9. k-NN10. DTW * 참고로 "밑바닥부터 배우는 데이터과학" 서적은 numpy,scikit-learn 등의 외부라이브러리를 활용은 배제되었습니다. 여기서 배울 베이즈 이론의 경우 데이터 분석 및 요즘 유행하고 있는 딥러닝 및 뇌과학에서도 핵심에 있는 중요한 이론입니다.박문호 박사님의 아래 동영상에서는 모든것은 베이즈로 이루어져 있다고도 말합니다. 시간 날때 함 보세요 재밌습니다.-> 뇌과학으로 본 인공지능의 현주소와 미래..
파이썬으로 클라우드 하고 싶어요 (http://www.slideshare.net/yongho/2011-h3) 2011년 발표니 꽤 된 내용이지만 굉장히 깔끔하게 잘 정리 되 있네요.최근에 파이썬으로 분산,병렬 컴퓨팅하는 방법에 대해 개인적으로 다시 정리 할 예정이고 아래 대략 메모. 사실 어떻게 보면 굉장히 명쾌하다. 하둡/스파크같은 시스템을 직접 만들려고 하면 어렵지만 ㅎㅎ확장 순서는 이렇게 될 꺼 같다. 1. 자신의 컴퓨터에서 단일 프로세스로 자신이 만든 데이터 분석 프로그램을 돌린다.2. 자신의 컴퓨터에서 멀티쓰레드로 자신이 만든 데이터 분석 프로그램을 돌린다.3. 자신의 컴퓨터에서 멀티 프로세싱으로 자신이 만든 데이터 분석 프로그램을 여러개 돌린다.4. 고성능 파이썬등의 책을 참고하든지 최대한 성..
파이썬의 함정 - 1 (부제: 나의 삽질기) 클래스 변수와 객체 변수에 대한 함정 자바나 C++ 베이스에서 파이썬으로 옮겨 왔을때 가장 실수하기 쉬운 부분에 대해서 살펴보겠습니다.먼저 아래 코드를 보시죠.class Test : num = 0 def show(self): print 'num :' + str(num) t = Test() t.show()어떻게 될까요? 에러입니다.어디서?print 'num :' + str(num)네 여기에서 num 를 못찾아서 에러가 납니다. 클래스 변수 num 을 찾지 못하네요.이걸 해결하려면 print 'num :' + str(self.num)이렇게 self 를 붙여 주어야 하는데요.self 는 JAVA나 C++에서 this 와 같으며 현재 객체를 말합니다. print 'n..
